On raconte que le mathématicien Vaughan Jones (1952–2020), conférencier d’honneur au Palais Corsini de Rome, est monté sur scène, s’est allumé un cigare et s’est mis à faire des ronds de boucane. C’était un clin d’œil à Peter Guthrie Tait, un des pionniers de la théorie des nœuds au 19e siècle. Ce dernier avait été fasciné par les cercles mouvants de fumée et s’en était inspiré pour élaborer sa théorie des nœuds.
Le nœud en mathématiques est très similaire au nœud familier. Il en a les croisements et la souplesse. Toutefois, les extrémités du nœud mathématique doivent être fusionnées, de sorte que le nœud ne peut pas se défaire. On a aussi inventé le non-nœud, ou nœud trivial, qui n’est en fait qu’un anneau. Tout comme le zéro en mathématique, il est nécessaire dans les calculs.
Depuis longtemps les mathématiciens et mathématiciennes se butent aux distorsions d’un nœud. Comme il est souple, on peut le manipuler jusqu’à ce qu’il soit totalement méconnaissable. On peut facilement retrouver la forme initiale d’un nœud à 3 croisements mais pas d’un nœud à 10 croisements. On a trouvé des façons de les trier, de les classifier, mais ce n’était pas suffisant. Il fallait un moyen de définir un nœud, peu importe sa configuration. Il fallait identifier les invariants, c’est-à-dire ce qui ne change pas dans un nœud malgré les distorsions.
Les polynômes de Jones définissent les nœuds et ce faisant ont amené la théorie des nœuds dans une tout autre direction.
Quelques exemples des polynômes de Jones
Le non-nœud

Le nœud de trèfle

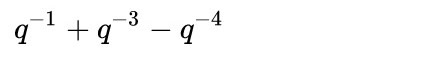
Le nœud en huit

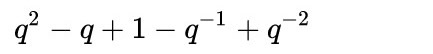
Le nœud pentacle, ou d’étoile
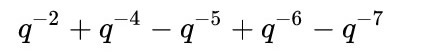
Le nœud de vache, bouts liés

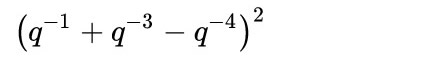
Le nœud plat, bouts liés
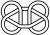
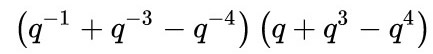
La théorie des nœuds peut nous apparaître comme un passe-temps, un loisir de mathématicien, mais loin de là. Les mathématiques ont idéalisé le nœud en le définissant comme une courbe fermée dans l’espace. La porte était ouverte à des applications plus vastes, dans d’autres sphères scientifiques.
Vaughan Jones est un géant dans l’histoire des mathématiques. Ses travaux ont permis de faire le pont entre les nœuds et la physique quantique. Les polynômes de Jones peuvent s’appliquer au comportement des particules anyons. Ils serviront peut-être à construire les futurs ordinateurs quantiques. Les vieux marins n’y croiraient rien.
Prochainement…

À la recherche d’un nom pour le bonnet turc, suite et fin.
Où les mathématiques, le billard et les noeuds tubulaires se rencontrent.
The Rolfsen Knot Table Mosaic, The Knot Atlas. Cette base de données de la théorie mathématique des noeuds est maintenue par l’Université de Toronto. C’est un wiki collaboratif dans l’esprit de Wikipedia.
Les nœuds y sont classés par le nombre de croisements. Dans le tableau on montre les nœuds de 0 à 10 croisements.
Pour vous divertir, une vidéo très intéressante de Mickaël Launay: Une énigme de 50 ans résolue : le nœud de Conway n’est pas bordant.
Il doit expliquer la théorie des nœuds avant de parler du nœud de Conway, un nœud récalcitrant qu’une mathématicienne, Lisa Piccirillo, a réussi à réussi à résoudre en quelques soirées.










2 Responses
Monsieur Flammèches, hum… hum… s’il y avait un espace de consultation avec divan sur ce site, je vous inviterais à vous y étendre et vous poserais quelques questions, notamment:
À quand remonte… hum… cet intérêt pour les noeuds?
Votre enfance… hum… évoque-t-elle pour vous des sensations liées à des noeuds?
Voyez-vous l’existence comme un noeud, hum… enfin… comme une énigme complexe à résoudre?
Hum…
S. F.
Euh… une affaire de gars, paraît-il. C’est enthousiasmant, non?